아이콘은 특정한 기능, 개념, 또는 대상을 상징하는 시각적 기호를 의미한다. 컴퓨터 그래픽 사용자 인터페이스(GUI)에서는 프로그램이나 폴더 등을 나타내는 시각적 기호로 사용되며, 일상생활에서는 표지판, 로고, 이모티콘 등 다양한 형태로 접할 수 있다. 아이콘은 정보를 빠르고 정확하게 전달하고, 화면공간을 효율적으로 사용하며, 사용자의 인지 및 기억을 돕는다는 장점이 있다(Kacmar and Carey, 1991; Lee, 1991). 이러한 장점으로 인해 아이콘은 데스크탑 컴퓨터부터 모바일 기기, 산업용/가정용 전자 제품에 이르기까지 다양한 플랫폼에서 폭넓게 사용되며, 그 사용빈도는 계속해서 증가하고 있다(Shao et al., 2024; Zeng and Bao, 2024).

이러한 추세에 따라 아이콘에 대한 다양한 인간공학적 연구들이 활발히 수행되고 있다(Huang et al., 2002; McDougall et al., 2016; Zhao et al., 2023). 아이콘 연구는 크게 아이콘 디자인과 아이콘 배치 문제로 구분할 수 있다. 아이콘 디자인은 전달하려는 정보를 시각적으로 어떻게 효과적으로 표현하고, 사용자가 이를 쉽게 인지하고 해석할 수 있도록 설계할 것인지에 대한 논의를 포함한다(Lim et al., 2006; McDougall et al., 2016). 반면에, 아이콘 배치 문제는 수많은 아이콘 속에서 사용자가 목표 아이콘을 신속하고 정확하게 찾도록 화면을 어떻게 구성하고 배열해야 하는지에 초점을 둔다(Bouwman and Brumby, 2020; Niemelä and Saarinen, 2000). 그런데 이러한 연구에서 사용되는 핵심적인 평가 방법은 사용자의 아이콘 탐색 수행도, 다시 말해 아이콘 시각탐색 능력을 측정하는 것이다.

본 연구는 아이콘 탐색 데이터의 분석 방법에 주목한다. 일반적인 아이콘 연구에서 탐색 수행도는 사용자가 목표 아이콘을 찾는 데 걸린 탐색시간을 의미하며, 반복적인 탐색과제를 통해 여러 건의 반응 시간 데이터를 수집한다. 이후 이 탐색시간의 산술평균을 대표 값으로 사용하여 아이콘 탐색 수행도를 평가하게 된다. 시각적 탐색작업에서는 목표를 우연히 매우 빠르게 발견하는 경우와 상대적으로 긴 시간이 소요되는 경우가 공존하기 때문에, 단일 대표 값으로 산술평균을 사용하는 것이 관례라고 할 수 있다. 그러나 산술평균을 대표 값으로 사용한다는 것은 반응 시간이 정규분포를 따른다는 가정한 것이다. 만약 탐색시간 데이터들이 정규분포를 하지 않고, 다른 형태의 확률분포를 보인다면, 산술평균의 사용은 데이터 분석 및 해석상의 오류를 유발할 수 있다.

아이콘 탐색 연구에서 탐색시간의 확률분포를 직접 측정한 사례는 찾기 어렵다. 그러나 유사한 인지 및 시각탐색 연구에서는 반응 시간이 따르는 확률분포에 대한 논의는 활발히 이루어져 왔다. 먼저, 인지적 과제에서 반응 시간 데이터의 정규성에 의문을 제기하는 다수의 논문이 발표되었다(Guy et al., 2020; Luce, 1991; Parris et al., 2013; Van Zandt, 2000). 이 연구들은 반응 시간이 정규분포보다는 ex-Gaussian 분포를 한다고 가정하는 것이 더 적절하다는 결과를 도출했다. 또한, 아이콘 탐색과 더 밀접한 시각탐색 연구에서도 반응 시간의 정규성 분석이 이루어졌다. 해당 연구들은 반응 시간 데이터가 우측 꼬리가 긴 양의 왜도(positive skew)를 가진 분포 형태를 보임을 확인하였으며, 데이터 분포를 정규분포보다는 ex-Gaussian 분포로 보는 것이 더 타당하다는 결과를 제시했다(Palmer et al., 2011; Park and Hyun, 2014).

본 연구의 주제인 아이콘 탐색작업은 시각탐색작업의 일종이라고 할 수 있다. 그러나 상기된 시각탐색 반응시간 분포에 대한 연구는 심리학 분야에서 주 연구대상인 단순 세부특징 탐색(Simple feature search)과 결합탐색(conjunction search)이다(Treisman and Gelade, 1980; Treisman and Sato, 1990; Wolfe et al., 1989). 이런 형태의 시각탐색작업은 비교적 탐색 난이도가 낮은 작업이라고 할 수 있다. 탐색공간에 있는 방해 자극과 표적은 한 개 또는 두 세 개의 특징(features)의 조합으로 구성되어 있다. 이런 탐색공간에서 표적을 찾는 시각탐색작업이다. 그러나 아이콘 탐색작업의 탐색공간에 있는 아이콘들은 다수의 특징(features)의 혼합으로 구성되어 있다. 즉 아이콘 탐색작업은 단순 세부특징 탐색과 결합탐색보다 탐색 난이도가 더 높다고 할 수 있다. 탐색 난이도가 더 높은 아이콘 탐색작업에서의 반응 시간은 어떤 분포를 하는지 확인하는 것이 필요하다.

한편, 인간공학 분야에서 1960년대부터 연구되어온 시각탐색작업은 시각적 품질검사작업이다. 제품이나 부품 상에 특정한 결함을 눈으로 탐색하고, 결함을 발견하였을 때 불량품으로 처리하는 작업이다. 특정한 제품에서 결함을 찾는데 소요되는 시간은 우연히 단시간 내에 발견할 수도 있지만, 많은 경우에는 제품(탐색공간)을 여러 번 반복적으로 탐색해야만 제품 상의 결함을 발견할 수 있다. 심지어 어떤 경우에는 결함이 존재함에도 불구하고 발견을 하지 못하는 경우도 있다. 시각적 품질검사 연구에서 반응 시간의 분포는 변형된 지수분포 형태로 가정하였으며, 대표 값으로 산술평균 대신에 기하평균탐색시간(GMST: Geometric Mean Search Time)을 사용해왔다(Morawski et al., 1980; Drury and Watson, 2002; Lee and Hong, 2011).

본 연구에서의 관심은 아이콘 탐색시간이 ex-Gaussian 분포하는지, 아니면 변형된 지수분포를 하는지 알아보는 것이다. 또한 아이콘 탐색시간과 정규분포와의 적합성도 검토하려고 한다. 한편, 아이콘 탐색작업 내에서도 탐색 난이도는 탐색작업의 형태에 따라 차이가 있을 수 있다. 특정한 형태의 아이콘 탐색작업만을 실험 대상으로 설정했을 때 생기는 일반화의 오류를 최소화하기 위해 다양한 아이콘 탐색작업을 대상으로 실험을 실시할 예정이다. 추가적으로 세가지 분포로부터 도출된 기대치들(평균)을 활용하여, 아이콘 탐색시간에 영향이 미치는 요인들을 분석하고 비교하려고 한다. 세가지 분포를 가정했을 때 도출된 기대치를 상이할 수 있고, 상이한 기대치로 인해 아이콘 탐색시간에 영향을 미치는 요인에 대한 통계분석 결과가 달라질 수 있기 때문이다. 즉 도출된 기대치를 사용하여 분산분석을 실시하고 통계적 유의성을 비교하려고 한다.

어떤 데이터에서 양의 왜도 현상이 나타나는 경우에 적합도가 높은 여러 가지 확률분포들이 있을 수 있다. 본 연구에서는 기존 시각탐색 연구에서 검토된 적이 있는 두 가지 확률분포, ex-Gaussian 분포와 변형된 지수분포를 대상으로 아이콘 탐색시간의 분포 적합도를 검증하려고 한다. 추가적으로 정규분포의 적합도도 검증하려고 한다. 단지 본 논문에서는 정규분포의 소개는 생략한다.

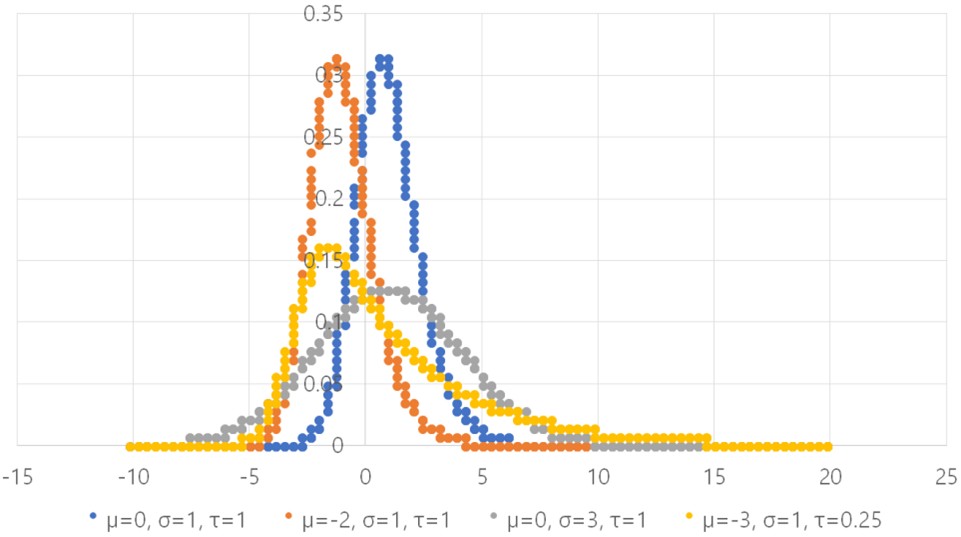
Ex-Gaussian 분포는 정규분포(평균 μ, 표준편차 σ)와 지수분포(평균 τ)의 합성으로 정의된다. 식 (1)은 ex-Gaussian 분포의 확률밀도함수를 나타내며, 평균은 μ+τ이고 분산은 이다. 여기서 μ는 정규분포의 평균, σ는 정규분포의 표준편차, τ는 지수분포의 평균, 그리고 Φ는 표준정규분포의 누적분포함수를 나타낸다. Figure 1은 ex-Gaussian 분포의 확률밀도함수 그래프이며, 관련된 모수들을 변화시킬 때 다양한 모양의 분포가 나타난다는 것을 알 수 있다.

Figure 1. Probability density functions of the ex-Gaussian distribution (Example parameters)

Modify Delete

시각적 품질검사는 인간공학 연구 분야에서 항공기 검사, 철판검사, PCB 검사 등 다양한 제품을 검사할 때 인간의 시각적 검사능력과 오류를 연구하였다(Drury, 1975). 시각적 품질검사 시간의 평균값은 일반적인 산술평균을 사용하지 않고, 기하평균탐색시간(GMST: Geometric mean search time)을 사용해 왔다. Monk (1976)에 의해 제안된 GMST는 변형된 지수분포의 평균치를 의미한다. 이후에 시각적 품질검사를 연구하는 많은 연구자들은 GMST를 시각탐색 시간의 평균값으로 사용해 왔다(Chan and So, 2007; Drury and Hong, 2000; Gallwey, 2009). 다음은 시각적 품질검사 시간의 변형된 지수분포와 평균값을 도출하는 과정의 사례다.

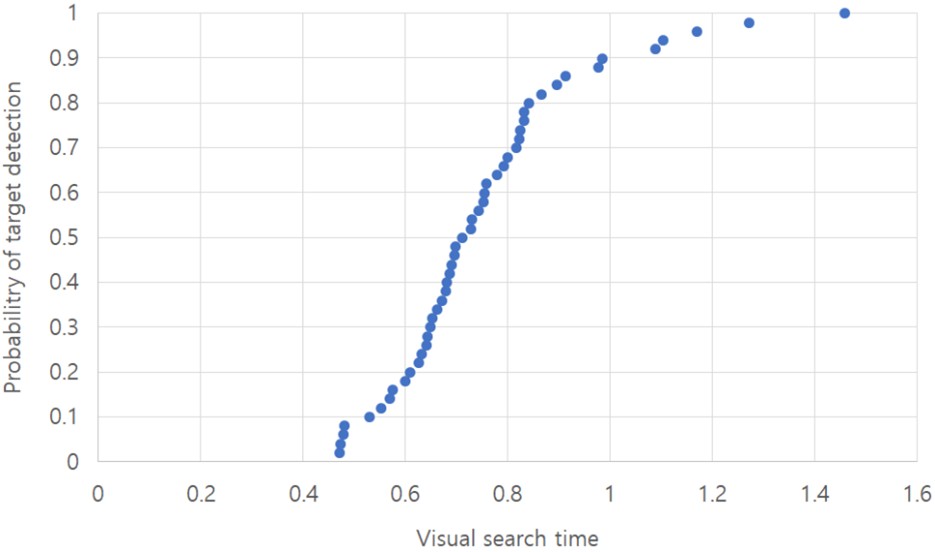
예를 들어, 50회의 시각적 품질검사 시간이 수집되었다면, 먼저 검사시간을 작은 수부터 큰 수로 오름차 순으로 정렬한다. 짧은 시간은 매우 신속히 결함을 찾았다는 것을 긴 시간은 결함을 찾는데 오래 시간이 소요되었다는 것을 의미한다. 만약 품질검사 시간을 짧은 시간으로 제한한다면 검사자는 결함을 찾을 확률은 매우 낮을 것이다. 반면에 매우 긴 검사시간이 검사자에게 주어진다면 어떤 결함이 있을지라도 찾을 확률은 거의 100%일 것이다. 이러한 상황을 가정하여 오름차순으로 정렬된 검사시간에 찾을 확률을 매칭시킬 수 있다. 가장 긴 검사시간에는 0.999 확률을 가장 짧은 검사시간에는 0.020 확률을 매칭시키고, 다른 검사시간에는 균일한 간격으로 확률을 매칭시킨다. Table 1의 2열의 검사시간과 3열의 결함을 찾을 확률을 그래프로 표시하면, Figure 2와 같은 지수분포의 누적 확률함수가 된다.

Figure 2. Cumulative probability density function of the exponential distribution

Modify Delete

지수분포의 누적 확률밀도함수는 수식(2)와 같이 표현될 수 있다.

도출된 지수분포의 누적 확률함수에서 평균치 1/λ 값을 구하고 이 값을 GMST라고 한다. GMST는 통상적인 지수분포의 평균과는 다르다. 수집된 데이터에 임의의 확률을 매칭시켰기 때문이다.

수집된 데이터로부터 λ를 구하기 위해, 수식(2) f(x|λ)를 확률 p로 치환하고, 지수함수를 우변에 두고 정리하면 수식(3)이 된다. 수식(3)의 양변에 자연로그 함수를 취하며 수식(4)이 되고, 수식(5)로 변환시킬 수 있다. 즉 수식(5)는 λ 기울기로 하는 선형 회귀식이며 ε은 에러항이다.

Table 1의 3열 -ln (1-p)와 탐색시간 데이터를 그래프로 표시하면 Figure 3과 같다. 한편 도출된 선형회귀식은 수식(6)이다.

Figure 3. Linear regression analysis to find λ

Modify Delete

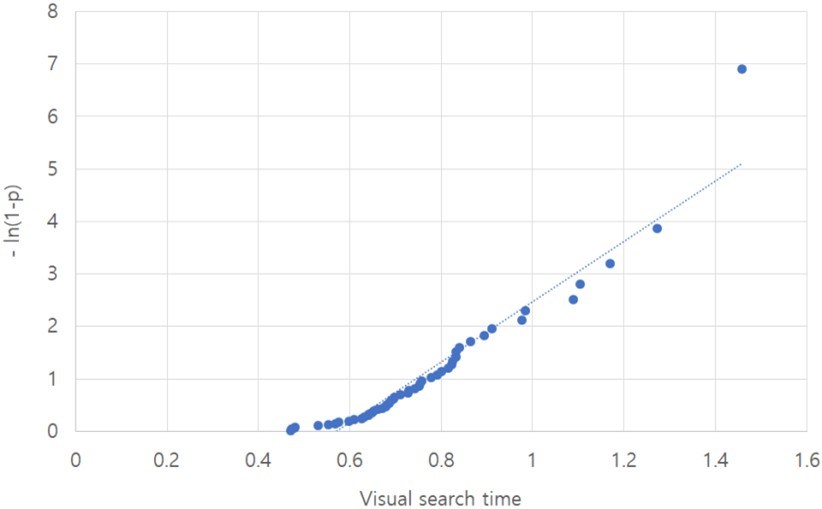
여기서 1/λ은 지수분포의 평균이며 0.174다. X축의 절편은 -ε/λ이다. X축 절편은 표적을 탐색하기 위해 소요되는 준비시간을 의미한다. 예를 들어 표적을 발견하고 마우스로 표적을 클릭한다면, 클릭할 때 소요되는 시간이다. 이 시간은 순수한 표적 탐색시간이 아니지만 수집된 탐색시간 데이터에 항상 포함되는 시간이다. 통상적으로 ε는 음수를 갖는다. 최종적으로 기하평균탐색시간(GMST)은 1/λ – ε/λ이 된다. 사례에서 GMST는 0.774가 된다. 지수분포의 적합도는 선형회귀식의 적합도에 의해 결정된다.

3.1 Participants

본 실험의 참가자는 대학교에 재학 중인 학생들이었으며, 총 11명(남성 11명)이다. 참가자의 연령은 평균 23.34세이고, 이들의 시력이 모두 정상 또는 정상으로 교정되었다. 참가지들은 매일 컴퓨터 작업을 수행하고 있기 때문에 아이콘을 탐색하고 클릭하는 과제에는 익숙하였다.

3.2 Stimuli and apparatus

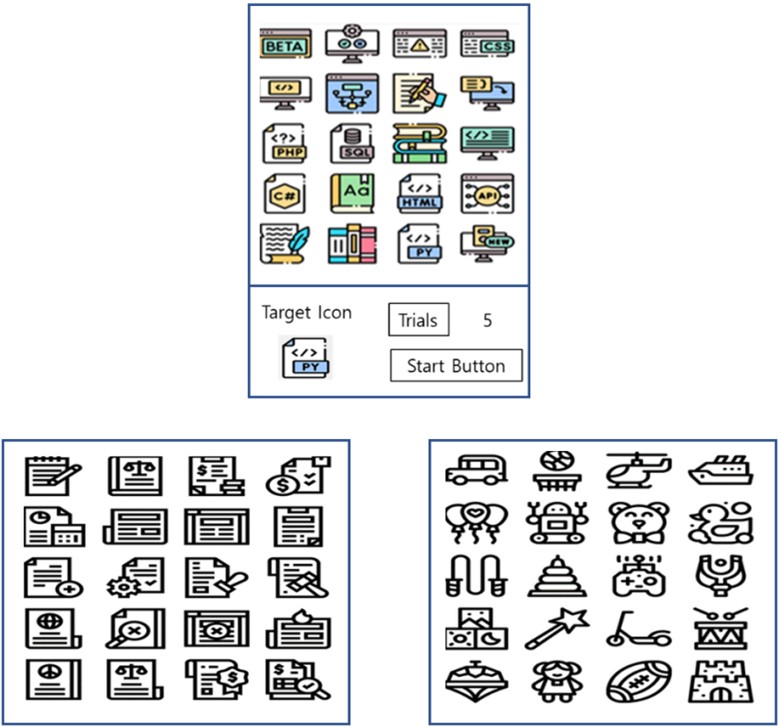
본 실험은 Intel i7 프로세서와 Windows 11 운영체제가 설치된 데스크톱 컴퓨터(AMD Ryzen 7 5800X, 8-Core CPU)를 사용하여 수행하였다. 시각 자극은 34인치 LCD 모니터(해상도: 3,440 × 1,440 픽셀, 재생률: 75Hz)를 통해 제시되었다. 아이콘 탐색을 위한 자극은 모니터의 중앙에 제시되었으며, 시작버튼을 누르면 실험이 시작되었고, 동시에 표적 아이콘과 배경 아이콘이 표시되었다. Figure 4의 상단 그림은 배경 아이콘, 표적 아이콘, 반복횟수, 시작버튼의 위치를 나타내고 있다. 참가자가 표적 아이콘을 찾으면, 마우스로 표적 아이콘을 클릭하였다. 표적 아이콘을 클릭한 시간은 표적 아이콘 탐색시간으로 기록되었다. 반복실험에서 마우스로 표적 아이콘을 클릭하면, 반복횟수로 증가하였고 동시에 다음 실험을 위해 배경 아이콘의 위치는 랜덤하게 바뀌었으며, 목표 아이콘도 배경 아이콘 중에 하나가 랜덤하게 선택되어서 나타났다. 본 실험을 위한 자극과 장치는 Python으로 제작하였다.

Figure 4. Examples of background icon for this experiment: 20 colored icons (top), 20 similarly shaped black and white icons (bottom left), and 20 different black and white icons (bottom right)

Modify Delete

3.3 Design of experiments

본 실험을 시행하기 전에 참가자들은 15분 간의 아이콘 탐색 연습을 하였다. 본 실험은 다양한 형태의 아이콘 탐색작업을 포함할 수 있도록 설계하였다. 본 실험은 2개의 블록으로 구성되었다. 참가자들은 두 개의 블록실험을 모든 참여했다. 첫 번째 블록실험은 배경 아이콘의 수와 배경 아이콘의 색상을 변화시키면서 실험을 수행하였다. 배경 아이콘의 수는 3수준으로 6개, 20개 50개로 변화시켰다. 그리고 배경 아이콘의 색상은 2수준으로 칼라 색상인 경우와 흑백 색상의 경우로 구분하였다. 두 번째 블록실험은 배경 아이콘의 모양의 유사성을 변화시키면서 실험을 진행하였다. 배경 아이콘의 색상은 흑백이며, 아이콘의 수는 20개로 한정하였다. Figure 4의 하단 그림은 배경 아이콘의 예을 보이고 있다. 각 참가자는 블록 1과 블록 2의 각 실험조건에서 50회의 반복실험을 수행하였다. 실험과정에서 수집된 측정값은 표적 아이콘의 탐색시간이다. 각 참가자가 수행한 아이콘 탐색실험의 총 횟수는 400회였다(블록 1: 3(아이콘 수) × 2(색상) × 50 = 300회, 블록 2: 2(아이콘 모양 유사성) × 50 = 100).

4.1 Goodness-of-fit analysis of probability distributions for visual search times

아이콘 탐색시간의 확률분포 적합도를 검정하기 전에 각 실험조건에서 11명의 참가자로부터 측정한 50회의 아이콘 탐색시간의 왜도(skewness)를 분석하였다. 왜도(skewness)는 데이터 분포의 좌우 비대칭성을 나타내는 통계량이다. 분포가 오른쪽으로 치우쳤으면 왜도가 양수이고, 왼쪽으로 치우쳤으면 왜도가 음수이며, 좌우가 대칭인 정규분포의 왜도는 0이다. 즉 데이터가 특정 방향으로 얼마나 몰려 있는지를 파악하는 데 사용된다. 모든 실험조건에서 양의 왜도 현상이 나타났다. 일반적인 시각탐색 실험에서 나타나는 양의 왜도 현상이 아이콘 탐색시간에서도 나타나고 있다고 할 수 있다.

왜도 값이 실험조건별로 유의한 차이가 있는지 검토하기 위해 분산분석을 실시하였다. 실험 블록 1에서 색상(F(1, 60) = 1.08, p = 0.303), 아이콘의 수(F(1, 60) = 0.63, p = 0.538)에 따라 왜도 값이 유의하게 차이가 없었으며, 실험 블록 2에서 아이콘의 유사성(F(1, 20) = 2.08, p = 0.164)에 따라 왜도 값도 유의한 차이가 없었다. 즉 특정한 실험조건에서 왜도 값이 더 크게 나타나지는 않는다는 것을 의미한다. Figure 5는 각 실험조건별 왜도의 평균값을 나타낸다.

Figure 5. Mean skewness values for each experimental condition: experiment block 1 conditions on the left and experiment block 2 conditions on the right

Modify Delete

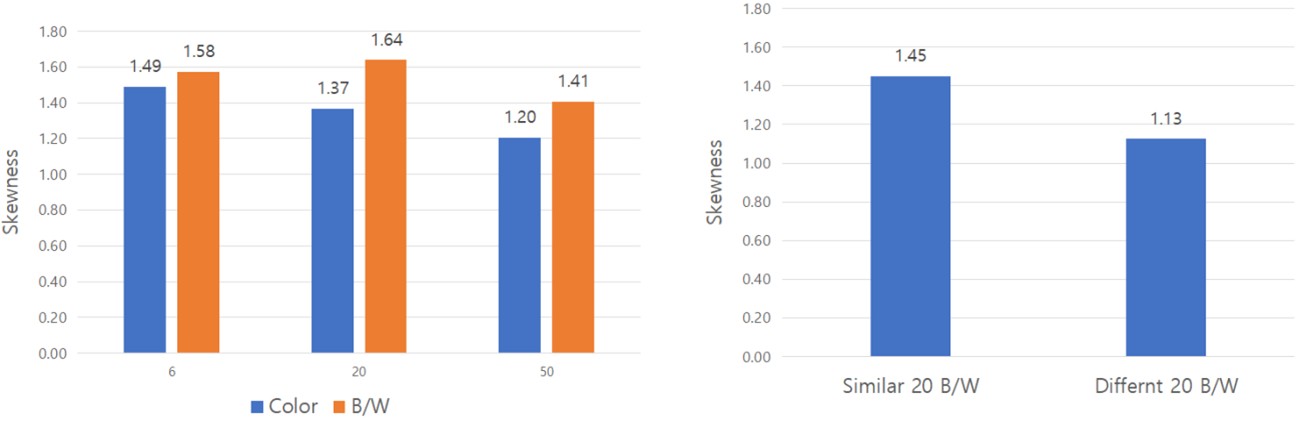
다음으로 아이콘 탐색시간이 3가지 확률모형 적합도를 검정하였다. 정규분포와 ex-Gaussian 분포의 적합도 검정을 위해 Komogorov-Simirmov (K-S test)를 실시하였다. 그리고 변형된 지수분포는 2절에서 설명한 바와 같이 탐색시간과 변형된 탐색확률의 선형회귀분석을 통해 적합도를 검정하였다. Table 2은 적합도 검정의 결과를 나타낸다. 정규분포의 적합도가 p < 0.05인 경우는 실험조건에 따라 차이가 있었지만, 9.0%에서 36.4% 사이였다. 즉 아이콘 탐색시간이 정규분포라고 할 수 없는 경우가 많이 나타났다. ex-Gaussian 분포의 적합도 검정결과는 모든 실험조건에서 ex-Gaussian 분포의 적합도가 0.05 이상이었다. 즉 아이콘 탐색시간은 ex-Gaussian 분포를 한다고 할 수 있다. 또한 변형된 지수분포의 적합도도 높았다. 선형회귀분석 결과, 결정계수가 0.85 이상이었으며, 모든 p 값이 0.001 이하였다. 아이콘 탐색시간은 변형된 지수분포를 한다고 할 수 있다.

4.2 A comparison of the effects of three visual search metrics

세가지 확률분포의 가정하에서 각 실험조건에서 아이콘 탐색시간의 기대치(평균치)들을 계산하였다. 먼저 이 평균값들을 사용하여 배경 아이콘 수의 증가에 따른 아이콘 탐색시간의 변화를 살펴보았다. 배경 아이콘의 수의 증가하면서 표적 아이콘 탐색시간의 평균치는 일정한 비율로 증가하였다. 이런 경향은 세가지 평균치 모두에서 나타났다. 수식(7)은 정규분포를 가정했을 때의 표적 아이콘 탐색시간의 변화를 나타내는 선형회귀선이며, 수식(8)과 수식(9)는 변형된 지수분포의 평균치(GMST)의 선형회귀식과 ex-Gaussian 분포의 평균치의 선형회귀식이다. 즉 어떤 확률분포를 가정할지라도 아이콘 탐색시간은 배경 아이콘의 숫자가 증가하면서 일정한 비율로 증가했다. Figure 6은 배경 아이콘 수의 변화에 따른 아이콘 탐색시간의 변화를 나타낸다.

Figure 6. Effects of the number of background icons on icon search time

Modify Delete

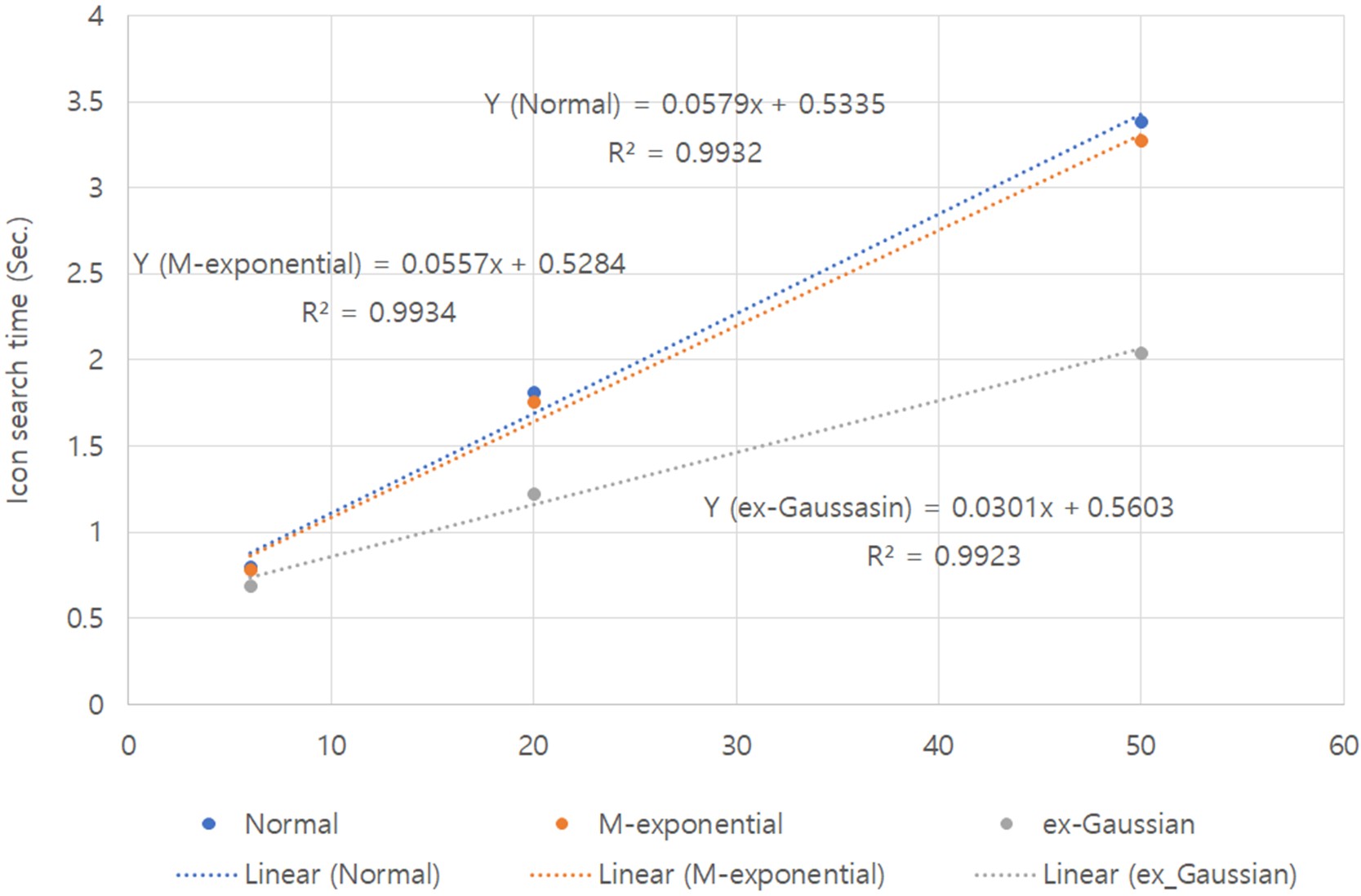
특징적인 결과는 정규분포와 변형된 지수분포를 가정했을 경우는 아이콘 탐색시간의 선형회귀식이 거의 동일하다는 것이다. 그러나 ex-Gaussian 분포를 가정한 경우에는 기울기가 작은 선형회귀식이 나타났고, 아이콘 탐색시간이 짧은 경우에는 다른 평균값들과 유사하였지만, 탐색시간이 긴 경우에는 다른 평균값보다 현저히 작게 나타났다. 이러한 결과는 ex-Gaussian 분포를 가정한 평균값은 다른 확률분포를 가정했을 때 보다 더 보수적인 경향을 보인다고 할 수 있다.

다음으로 세가지 분포의 평균값을 사용하여 분산분석을 실시하였다. Table 3은 분산분산 결과를 나타낸다. 아이콘의 색상이 칼라인 경우와 흑백인 경우의 비교분석에서 ex-Gaussian 분포를 가정한 평균값은 통계적으로 유의한 차이를 보이지 않았다. 그러나 다른 분포를 가정한 경우는 유의한 차이를 보였다. 이러한 결과는 ex-Gaussian 분포를 가정한 경우에 다른 분포를 가정한 경우와는 다른 분산분석 결과가 도출될 수 있다는 것을 의미한다.

본 연구에서 아이콘 탐색과제의 난이도를 변화시키면서 다양한 아이콘 탐색실험을 실시하였다. 수집된 아이콘 탐색시간은 정규분포를 하지 않았다. 9%에서 36.4%의 데이터가 정규분포를 하지 않았다. 반면에 수집된 데이터와 ex-Gaussian 분포 그리고 변형된 지수분포와의 적합도는 유의하게 높았다. 이러한 결과는 아이콘 탐색시간을 정규분포 특성만으로 해석하기 보다는 지수분포의 특성을 추가해야 한다는 것을 의미한다. ex-Gaussian 분포가 정규분포와 지수분포의 합성된 분포이고, 수정된 지수분포도 지수분포의 일종이기 때문이다. 또한 수집된 모든 아이콘 탐색시간에서 나타나는 양의 왜도 현상은 이러한 현상을 뒷받침한다고 할 수 있다.

Park and Hyun (2014)는 단순 세부특징 탐색과 결합탐색에서 탐색시간이 ex-Gaussian 분포를 한다는 연구결과를 제시하였다. 탐색 난이도가 낮은 시각탐색작업에서 탐색시간이 ex-Gaussian 분포를 한다는 것을 의미한다. 그러나 본 연구의 결과는 탐색 난이도가 낮은 6개의 아이콘이 배치된 탐색공간 뿐만 아니라 50개의 아이콘이 배치된 탐색공간의 탐색시간도 ex-Gaussian 분포를 한다는 결과를 보였다. 한편, 기존연구에서 탐색 난이도가 매우 높은 시각적 품질검사에서의 반응 시간은 변형된 지수분포를 하였다. 그런데 본 연구의 결과에 의하면 아이콘 탐색작업의 탐색시간도 변형된 지수분포를 하였다. 결론적으로 아이콘 탐색시간은 ex-Gaussian 분포 뿐만 아니라 변형된 지수분포를 한다고 할 수 있다.

본 연구에서는 세가지 확률분포로부터 도출된 평균값을 사용하여 탐색공간의 아이콘 수, 아이콘의 색상 그리고 아이콘의 유사성이 탐색시간에 미치는 영향을 분석하였다. 첫째 탐색공간 내의 아이콘의 수가 증가하면서 비례적으로 세가지 평균탐색시간이 증가하였다. 선형회귀분석의 결정계수는 0.992 이상이었다. 그러나 정규분포 평균값과 변형된 지수분포 평균값을 사용할 때 선형회귀식의 기울기는 거의 동일했다. ex-Gaussian 분포의 평균값에서는 상대적으로 작은 기울기였다. 즉 아이콘의 수가 커졌을 때는 다른 분포와 비교할 때 평균값이 작았다. 이는 탐색 난이도가 클 때, 다른 분포 평균값에 비해 ex-Gaussian 분포 평균값은 작게 나타난다는 것을 의미한다.

한편, 아이콘의 색상이 탐색시간 평균값에 미치는 영향을 분석하기 위해 실시한 분산분석의 결과에서 정규분포 평균값과 변형된 지수분포 평균값은 통계적으로 유의한 차이를 보였다. 그러나 ex-Gaussian 분포의 평균값을 사용할 때는 유의한 차이를 보이지 않았다. 이러한 상반된 결과들은 아이콘 탐색시간을 분석할 때, 어떤 확률분포를 가정할 것인가와 관련하여 시사하는 바가 있다고 할 수 있다. 결론적으로 아이콘 탐색시간의 분포는 ex-Gaussian 분포와 변형된 지수분포로 가정하는 것이 바람직하다고 할 수 있다. 그러나 ex-Gaussian 분포의 평균값을 사용할 때 주의해야 하는 점은 탐색시간 난이도가 높은 경우에 다른 확률분포에 비해 작은 평균값을 제시한다는 것이다. 또한 분산분석 분석을 실시하는 경우에 다른 확률분포의 평균치를 사용할 때보다. 통계적으로 유의하지 않은 결과를 제시하는 경향이 있다는 것이다.